ฟังก์ชันขั้นบันได
จากวิกิพีเดีย สารานุกรมเสรี
ฟังก์ชันขั้นบันได คือฟังก์ชันบนจำนวนจริงซึ่งเกิดจากการรวมกันระหว่างฟังก์ชันคงตัวจากโดเมนที่แบ่งออกเป็นช่วงหลายช่วง กราฟของฟังก์ชันจะมีลักษณะเป็นส่วนของเส้นตรงหรือรังสีในแนวราบเป็นท่อน ๆ ตามช่วง ในระดับความสูงต่างกัน
เนื้อหา[ซ่อน] |
[แก้] นิยาม
ฟังก์ชัน f : R → R จะเรียกว่าฟังก์ชันขั้นบันได ถ้าฟังก์ชัน f สามารถเขียนให้อยู่ในรูปแบบนี้ได้-
 สำหรับทุกจำนวนจริง x
สำหรับทุกจำนวนจริง x
- ช่วงต่าง ๆ จะต้องไม่มีส่วนร่วมต่อกัน นั่นคือ Ai ∩ Aj = ∅ โดยที่ i ≠ j
- ยูเนียนของช่วงทุกช่วง คือเซตจำนวนจริงทั้งเซต นั่นคือ ∪i Ai = R
[แก้] ตัวอย่าง
- ฟังก์ชันคงตัวเป็นตัวอย่างอย่างง่ายของฟังก์ชันขั้นบันได ซึ่งประกอบด้วยช่วงเพียงช่วงเดียวคือ A0 = R
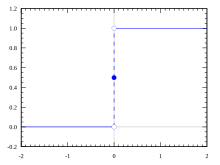
- ฟังก์ชันเฮฟวีไซด์ (Heaviside function) เป็นฟังก์ชันขั้นบันไดหนึ่งที่สำคัญ เป็นแนวคิดทางคณิตศาสตร์ที่อยู่เบื้องหลังการทดสอบสัญญาณไฟฟ้า เช่นที่ใช้ในการตอบสนองขั้นบันไดของระบบพลวัต
- ฟังก์ชันสี่เหลี่ยมมุมฉาก (rectangular function) ซึ่งเป็นฟังก์ชันรถตู้แบบบรรทัดฐาน (normalized boxcar function) เป็นอีกตัวอย่างหนึ่งของฟังก์ชันขั้นบันได ใช้เพื่อเป็นแบบจำลองของพัลส์หนึ่งหน่วย
[แก้] ในทางตรงข้าม
- ฟังก์ชันภาคจำนวนเต็ม ไม่ถือว่าเป็นฟังก์ชันขั้นบันไดตามนิยามที่ระบุในบทความนี้ เพราะมีจำนวนช่วงขั้นเป็นอนันต์ (n → ∞) ไม่เป็นจำนวนจำกัด
[แก้] สมบัติ
- ผลรวมและผลคูณของฟังก์ชันขั้นบันไดสองฟังก์ชัน จะให้ผลเป็นฟังก์ชันขั้นบันไดอีกฟังก์ชันหนึ่ง และผลคูณของฟังก์ชันขั้นบันไดกับจำนวนคงตัวก็ยังคงเป็นฟังก์ชันขั้นบันได จากกรณีทั้งสองทำให้ฟังก์ชันขั้นบันไดก่อร่างพีชคณิตขึ้นมาเหนือจำนวนจริง
- ฟังก์ชันขั้นบันไดมีจำนวนช่วงเป็นจำนวนจำกัดเท่านั้น ถ้าช่วง Ai ต่าง ๆ ซึ่ง i = 0, 1, …, n ตามนิยามข้างต้นไม่ทับซ้อนซึ่งกันและกัน และยูเนียนของช่วงทั้งหมดเป็นจำนวนจริง จะได้ว่า f (x) = αi สำหรับทุกค่าของ x ∈ Ai
- ปริพันธ์เลอเบกของฟังก์ชันขั้นบันได
 คือ
คือ  เมื่อ
เมื่อ  คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง Ai ทั้งหมดมีความยาวจำกัด ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก [1]
คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง Ai ทั้งหมดมีความยาวจำกัด ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก [1]
[แก้] อ้างอิง
- ^ Weir, Alan J. Lebesgue integration and measure. Cambridge University




![f = 0 \chi_{(-\infty, -5)} + 4 \chi_{[-5, 0]} + 7 \chi_{(0, 1)} + 3 \chi_{[1, 6)} + 0 \chi_{[6, \infty)}](http://upload.wikimedia.org/wikipedia/th/math/7/6/2/762c35786d6da8e31a1a2eb5c9c97bce.png)

ไม่มีความคิดเห็น:
แสดงความคิดเห็น